实现一棵AVL树

in 数据结构 with 2 comments

二叉树 平衡树 AVL

之前介绍过AVL（二叉排序树），但是只给出了思路没有j具体实现，本文将结合原来的一些树的知识，实现一棵AVL树。

回忆

在这之前，你可能还需要查看这些内容

二叉查找树：https://www.onesrc.cn/p/binary-search-tree.html

AVL树：https://www.onesrc.cn/p/avl-tree.html

如何优雅地打印二叉树-2：https://www.onesrc.cn/p/how-to-print-binary-tree-elegantly-2.html

思考

实现AVL树的核心是什么

AVL比普通二叉排序树多了一个平衡的特性，这个平衡需要用平衡因子去维护，所以平衡因子才是AVL的核心。如何计算和维护平衡因子也就成了关键部分。

如何度量平衡因子

度量方式当然是用左子树高度减去右子树高度啦！既然这样，那么就需要将子树的高度记录到子树上，以免每一次计算平衡因子时都需要重新计算两个子树的高度（当然这样也可以，只是工作量太大，有点浪费资源）。那么对于这棵树本身来说，它的高度又该为多少呢？一棵树的高度，等于它的子树中较大的那个加一，所以这棵树的高度就等于子树高度最大值加一。而对于叶节点来说，可以规定它的高度为1。

代码部分如下：

typedef struct Node{
    int data;
    int level;//比原来多了一个树的高度
    struct Node *l, *r;
}Node;
//计算一棵树的高度
void giveBal(Node* bt){
    if(bt->l==NULL&&bt->r==NULL){
        bt->level = 1;
    }else if(bt->l!=NULL&&bt->r==NULL){
        bt->level = bt->l->level + 1;
    }else if(bt->l==NULL&&bt->r!=NULL){
        bt->level = bt->r->level + 1;
    }else{
        bt->level = bt->l->level > bt->r->level ? bt->l->level+1 : bt->r->level+1;
    }
}
//根据树高计算平衡因子
int checkBal(Node* bt){
    if(bt->l==NULL&&bt->r==NULL){
        return 0;
    }else if(bt->l!=NULL&&bt->r==NULL){
        return bt->l->level;
    }else if(bt->l==NULL&&bt->r!=NULL){
        return 0-bt->r->level;
    }else{
        return bt->l->level - bt->r->level;
    }
}

单次旋转问题

我们知道在AVL的平衡性调整中，有两个非常重要的内容：左旋和右旋。

左右旋转是对称的，下面以右旋转为例进行说明。

如果需要对一棵树进行右旋，那么我们就需要将它的右子树的左子树部分放到放到它的左子树上，将它原来的左子树替代它变成新的父节点，并将原来的父节点变为新父节点的右子树。有点绕，看图慢慢品吧。

右旋转前：

1565704323786.png

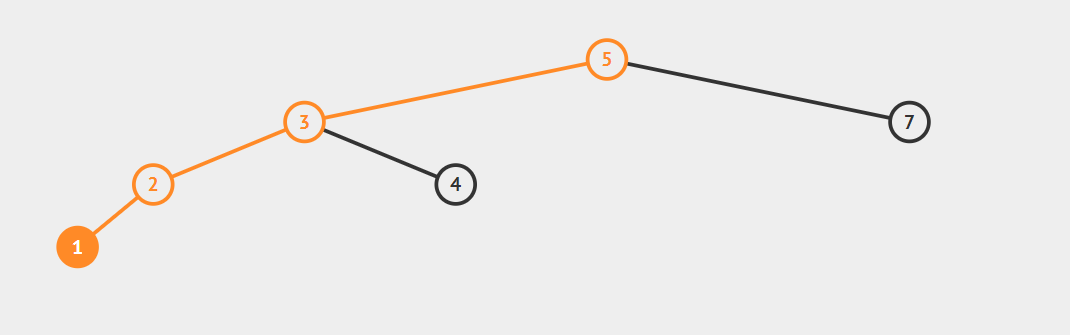
右旋转后：

1565704354700.png

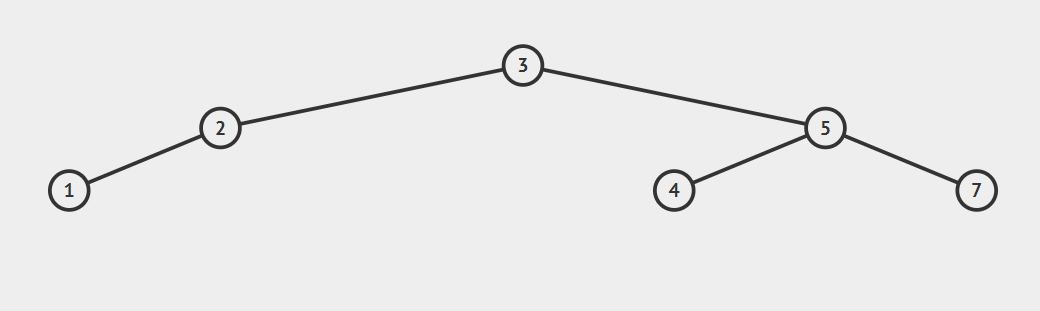
动图演示：

3443859613.gif

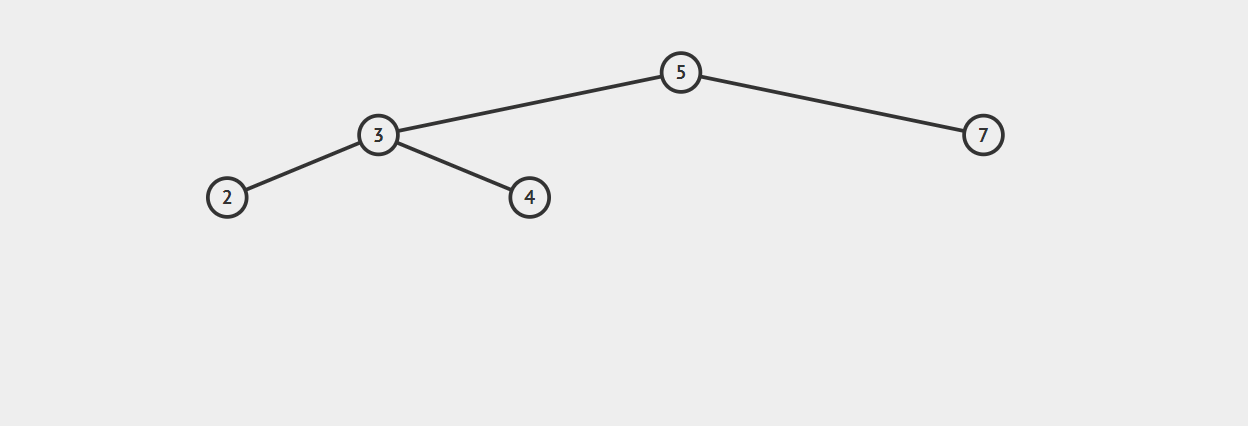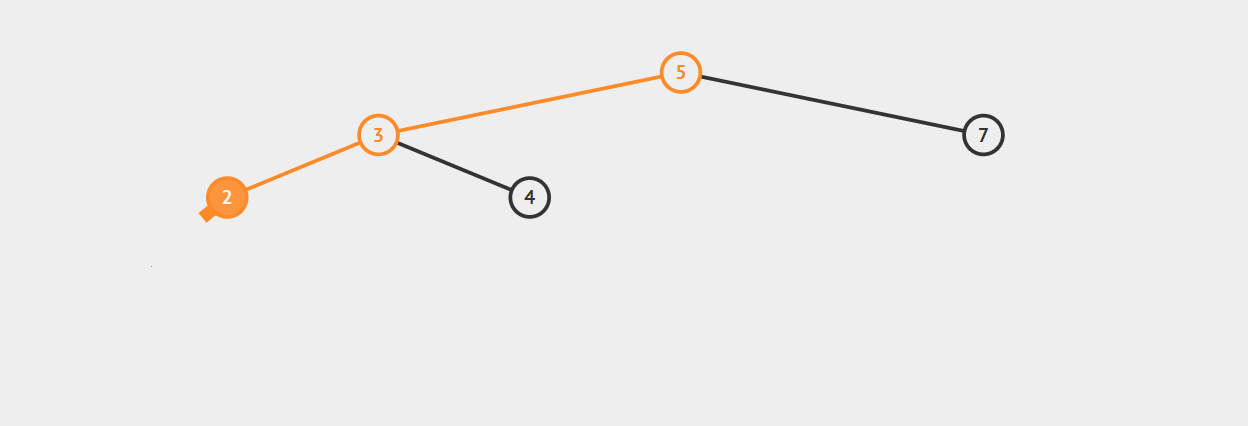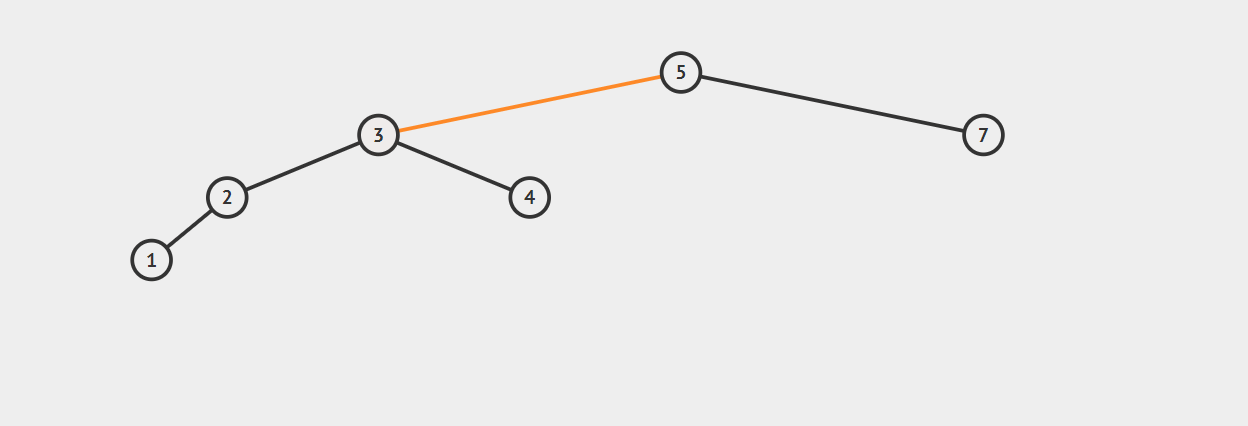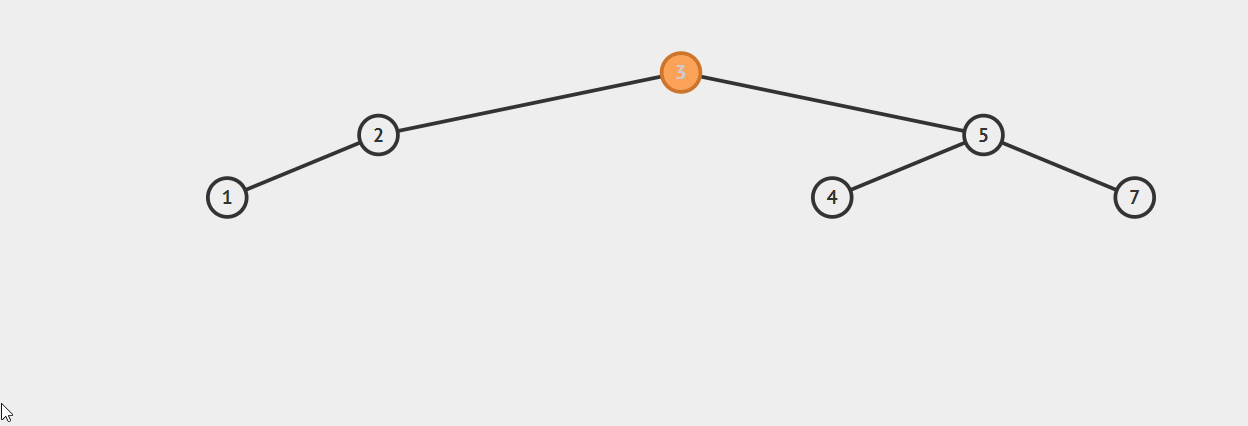
由于旋转的问题，部分树（原父节点、新父节点）的高度会发生改变，所以我们需要调用上面提到的树高计算函数giveBal()修正这两个节点的树高。

void rRotate(Node* &bt){
    Node *tmp = bt->l;
    bt->l = bt->l->r;
    tmp->r = bt;
    giveBal(bt);
    bt = tmp;
    giveBal(bt);
}

两次旋转问题

观察下面两个旋转，第一个图是LL型，进行一次右旋转即可平衡；第二个图是LR型，需要先进行一次左旋转，再进行右旋转，那么能不能把两种情况合并呢？

1565704323786.png

1565705026622.png

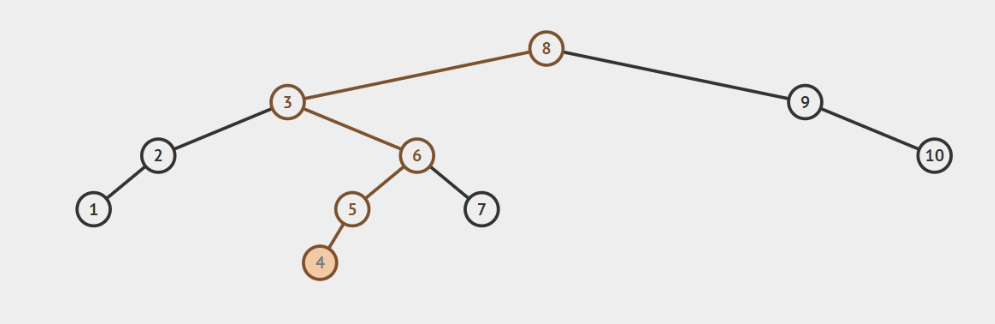
经过列举各种情况，可总结得到下表。

类型父节点平衡因子左子树平衡因子右子树平衡因子
LL21*
LR2-1*
RR-2*-1
RL-2*1

故此可以将LL和LR合并判断，如果左子树平衡因子小于0，则先进行一次左旋转，然后两种情况都需要进行一次右旋转。RR和RL同理。

void rotate(Node* &bt){
    int bal = checkBal(bt);
    if(bal<=1&&bal>=-1){
        return;//balance
    }else if(bal>1){
        if(checkBal(bt->l)<0){
            lRotate(bt->l);
        }
        rRotate(bt);
    }else if(bal<-1){
        if(checkBal(bt->r)>0){
            rRotate(bt->r);
        }
        lRotate(bt);
    }
}

插入调整

插入新节点，我们是利用递归实现的，那么在每一次插入新节点后，这条递归链所经过的每一个节点其高度都会改变，所以需要在函数结束的最后，对每一个节点重新进行高度的计算，并判断是否失衡，如失衡则进行旋转操作。（平衡二叉树的每一棵子树也是平衡二叉树，子树平衡是该树平衡的前提，所以要自下向上维护树的平衡性）。

void insertBST(Node *&bt,int k){
    if(bt==NULL){
        bt = (Node *)malloc(sizeof(Node));
        bt->key = k;
        bt->l = bt->r = NULL;
    }else if(k<bt->key){
        insertBST(bt->l, k);
    }else{
       insertBST(bt->r, k);
    }
    giveBal(bt);
    rotate(bt);
}

删除调整

删除和插入同理，也需要对递归链上的节点进行处理。

编码

代码部分

#include <stdio.h>
#include <stdlib.h>
#define MAXCOUNT 100
#define TREEARRAYCOUNT 10
#define key data
const int BPOW[] = {0, 1, 3, 7, 15, 31, 63, 127};
typedef struct Node{
    int data;
    int level;
    struct Node *l, *r;
}Node;



//---二叉树打印部分---
Node *nodeList[MAXCOUNT];//顺序存储二叉树
int nodeNum = 0;//记录二叉树数组的有效大小
void toList(Node * Node,int n){
    if( Node!=NULL){
        if(n>nodeNum)nodeNum = n;
        nodeList[n] = Node;
        toList(Node->l,2*n);
        toList(Node->r, 2 * n + 1);
    }
}
void printBlank(int n){//打印n个空白单位
    for (int i = 0; i < n; i++)
        printf(" ");//按需调整“    ”
}
void printBinTree(Node * oldTree[],int s,int t){
    int NodeCount = t - s + 1;
    int MaxL = -1;
    Node **tree = oldTree + s;
    Node* treeArray[TREEARRAYCOUNT][TREEARRAYCOUNT] = {};
    for (int i = 0; i < NodeCount;){//分层
        MaxL++;
        for (int j = 0; j <= BPOW[MaxL] && i < NodeCount;)
            treeArray[MaxL][j++] = tree[i++];
    }
    MaxL++;//Better view
    for (int k = 0; k <= MaxL; k++){//打印
        printBlank(BPOW[MaxL - k]);
         //BPOW[k]+i<NodeCount，一个不多，一个不少↓
        for (int i = 0; i <= BPOW[k]&& (BPOW[k]+i<NodeCount); i++){
            if(treeArray[k][i]!=NULL){
                printf("%d", treeArray[k][i]->data);//按需调整“    ”//,treeArray[k][i]->level
            }else
                printf("#");
            printBlank(BPOW[MaxL - k + 1]);
        }
        printf("\n");
    }
    printf("-----------------------------------\n");
}
void printT(Node* root){
    for (int i = 0; i < MAXCOUNT;i++){
        nodeList[i] = NULL;
    }
    nodeNum = 0;
    toList(root, 1);
    printBinTree(nodeList, 1, nodeNum);
}
//---二叉树打印部分 END---

//计算树高
void giveBal(Node* bt){
    if(bt->l==NULL&&bt->r==NULL){
        bt->level = 1;
    }else if(bt->l!=NULL&&bt->r==NULL){
        bt->level = bt->l->level + 1;
    }else if(bt->l==NULL&&bt->r!=NULL){
        bt->level = bt->r->level + 1;
    }else{
        bt->level = bt->l->level > bt->r->level ? bt->l->level+1 : bt->r->level+1;
    }
}
//检查平衡因子
int checkBal(Node* bt){
    if(bt->l==NULL&&bt->r==NULL){
        return 0;
    }else if(bt->l!=NULL&&bt->r==NULL){
        return bt->l->level;
    }else if(bt->l==NULL&&bt->r!=NULL){
        return 0-bt->r->level;
    }else{
        return bt->l->level - bt->r->level;
    }
}
//左旋
void lRotate(Node* &bt){
    Node *tmp = bt->r;
    bt->r = bt->r->l;
    tmp->l = bt;
    giveBal(bt);
    bt = tmp;
    giveBal(bt);
}
//右旋
void rRotate(Node* &bt){
    Node *tmp = bt->l;
    bt->l = bt->l->r;
    tmp->r = bt;
    giveBal(bt);
    bt = tmp;
    giveBal(bt);
}
//是否旋转
void rotate(Node* &bt){
    int bal = checkBal(bt);
    if(bal<=1&&bal>=-1){
        return;//balance
    }else if(bal>1){
        if(checkBal(bt->l)<0){
            lRotate(bt->l);
        }
        rRotate(bt);
    }else if(bal<-1){
        if(checkBal(bt->r)>0){
            rRotate(bt->r);
        }
        lRotate(bt);
    }
}

void insertBST(Node *&bt,int k){
    if(bt==NULL){
        bt = (Node *)malloc(sizeof(Node));
        bt->key = k;
        bt->l = bt->r = NULL;
    }else if(k<bt->key){
        insertBST(bt->l, k);
    }else{
       insertBST(bt->r, k);
    }
    giveBal(bt);
    rotate(bt);
}

Node * searchBST(Node * bt,int k){
    if(bt==NULL||bt->key==k){
        return bt;
    }else if(k<bt->key){
        return searchBST(bt->l, k);
    }else{
        return searchBST(bt->r, k);
    }
}

void deleteBST(Node * &bt ,int k){
    if(bt==NULL)
        return;
    if(bt->data==k){
        Node *pre,*tmp;
        if(bt->r==NULL){
            pre = bt;
            bt = bt->l;
            free(pre);
        }else if(bt->l==NULL){
            pre = bt;
            bt = bt->r;
            free(pre);
        }else{
            pre = bt;
            tmp = bt->l;
            while (tmp->r!=NULL) {
                pre = tmp;
                tmp = tmp->r;
            } // 找到左子树中最大的元素s
            bt->key = tmp->key;  //替代被删节点
            if (pre != bt)
                pre->r = tmp->l; 
            else
                pre->l = tmp->l;
            free(tmp);
        }
    
    }else if(bt->data>k){
        deleteBST(bt->l, k);
    }else{
        deleteBST(bt->r, k);
    }
    giveBal(bt);
    rotate(bt);
}

Node * createBST(int R[],int n){
    Node * bt = NULL;
    int i;
    for (i = 0; i < n;i++){
        insertBST(bt, R[i]);  
    }
    return bt;
}

int main(void){
    //int a[] = {3, 2, 8, 1, 5, 9, 4, 6, 10, 7}; //{8,3,9,2,6,10,1,5,7,4};
    //  char tree[16] = {'0','1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'};
    //int a[] = {5,3,4,2,1};
    int a[] = {7,5,9,2,6,8,10,1,4,3};
    Node *root = createBST(a, 10);
   // root->l->r = NULL;
    printT(root);
    deleteBST(root, 5);//删除节点5
    printT(root);
}

输出结果

               7
       4               9
   2       5       8       10       
 1   3   #   6   

-----------------------------------
               7
       4               9
   2       6       8       10       
 1   3   

-----------------------------------

本文由 ukuq 创作，采用 知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: Aug 13, 2019 at 10:45 pm

上一篇: 如何优雅地下载百度云
下一篇: Java命令行提示找不到入口
← → ↓ ↑
表达式树问题
数据结构
如何优雅地打印二叉树-2
积露为波
AVL树
数据结构
二叉查找树
数据结构
如何优雅地打印二叉树
积露为波
堆排序
数据结构
Responses
  1. StarDynasty

    悄悄路过，

    Reply
    1. ukuq
      @StarDynasty

      被我发现了哈,,,

      Reply