计数排序 - ONESRC

数据结构排序分配收集

和基数排序类似，计数排序也是一种非比较型整数排序算法，也是通过“分配”和“收集”来实现排序。

1.排序思路

开辟一个长度为maxVal-minVal+1的数组C，用来记忆各个数字的个数

分配： 扫描一遍原始数组，以当前值-minVal 作为下标，将该下标对应的的计数器加一

收集： 从计数器的第二个元素(C[1])开始，每一项和前一项相加，对所有的计数进行累加

反向扫描一遍原始数组，将元素 R[i]填充在新阵列的第C[R[i] - minVal]项，每放一个元素就将 C减去1，由于数组下标从0，所以-1需要在填充之前进行。这里采用反向填充保证了稳定性

另一种收集方案： 反向遍历计数器

2.排序算法

以c为例,从小到大排序。

#include <stdio.h>

void counting_sort(int R[], int n){
    int i, maxVal = 0, minVal = 0, tmp[n];
    for (i = 0; i < n; i++)//寻找、记录最值。
    {
        if (R[i] > maxVal)
            maxVal = R[i];
        else if (R[i] < minVal)
            minVal = R[i];
    }
    int count[maxVal - minVal + 1];//设置并初始化计数器数组
    for (i = 0; i < maxVal - minVal + 1; i++){
        count[i] = 0;
    }
    for (i = 0; i < n; i++){//分配
        count[R[i] - minVal]++;
    }
    for (i = 1; i < maxVal - minVal + 1; i++){//收集
        count[i] += count[i - 1];
    }
    for (i = n - 1; i >= 0; i--){
        tmp[--count[R[i] - minVal]] = R[i];
    }
    for (i = 0; i < n; i++){ //放回原数组
        R[i] = tmp[i];
    }
    //打印分配收集后的结果
    for (i = 0; i < n; i++){
        printf("%d ", R[i]);
    }
    printf("\n");
}

int main(void){
    int a[] = {75,23,98,44,57,12,29,64,38,82};
    counting_sort(a, 10);
    return 0;
}

输出结果：

12 23 29 38 44 57 64 75 82 98

反向遍历计数器：

#include <stdio.h>

void counting_sort(int R[], int n){
    int i, maxVal = 0, minVal = 0, tmp[n];
    for (i = 0; i < n; i++)//寻找、记录最值
    {
        if (R[i] > maxVal)
            maxVal = R[i];
        else if (R[i] < minVal)
            minVal = R[i];
    }
    int count[maxVal - minVal + 1];//设置并初始化计数器数组
    for (i = 0; i < maxVal - minVal + 1; i++){
        count[i] = 0;
    }
    for (i = 0; i < n; i++){//分配
        count[R[i] - minVal]++;
    }
    for (i = 1; i < maxVal - minVal + 1; i++){//收集
        count[i] += count[i - 1];
    }
    for (i = n - 1; i >= 0; i--){
        tmp[--count[R[i] - minVal]] = R[i];
    }
    for (i = 0; i < n; i++){ //放回原数组
        R[i] = tmp[i];
    }
    //打印分配收集后的结果
    for (i = 0; i < n; i++){
        printf("%d ", R[i]);
    }
    printf("\n");
}

void counting_sort2(int R[], int n){
    int i, maxVal = 0, minVal = 0;
    for (i = 0; i < n; i++)//寻找、记录最值
    {
        if (R[i] > maxVal)
            maxVal = R[i];
        else if (R[i] < minVal)
            minVal = R[i];
    }
    int count[maxVal - minVal + 1];//设置并初始化计数器数组
    for (i = 0; i < maxVal - minVal + 1; i++){
        count[i] = 0;
    }
    for (i = 0; i < n; i++){//分配
        count[R[i] - minVal]++;
    }
    int j, k = n-1;
    for (i = maxVal - minVal; i >=0; i--){//这里可以更改下整理方式，反向遍历计数器。
        for (j = count[i]; j >0 ;j--){
            R[k] = i + minVal;
            k--;
        }
    }
    //打印分配收集后的结果
    for (i = 0; i < n; i++){
        printf("%d ", R[i]);
    }
    printf("\n");
}

int main(void){
    int a[] = {1,2,2,3,6,8,6,5,2,9};
    counting_sort2(a, 10);
    return 0;
}

注：上述函数同样不适用于负数情况。

动图演示：

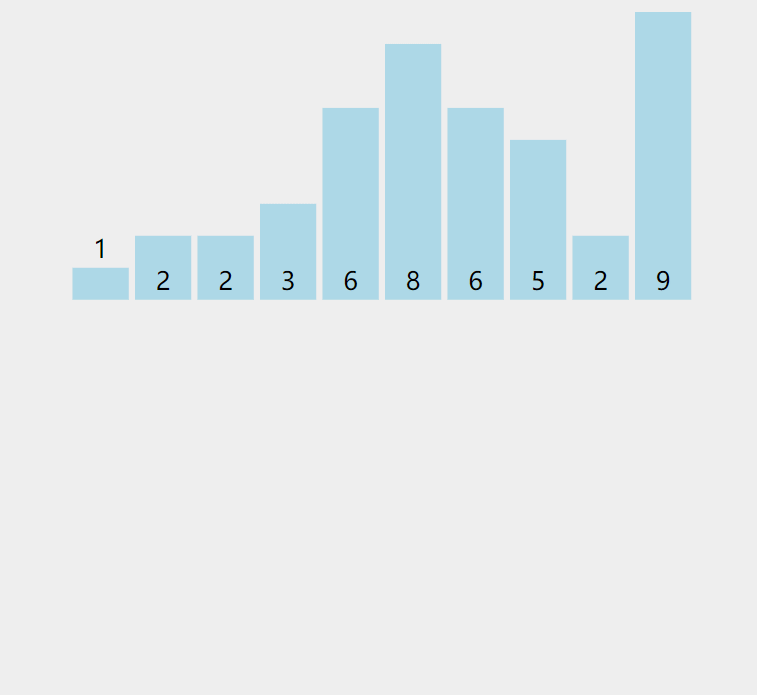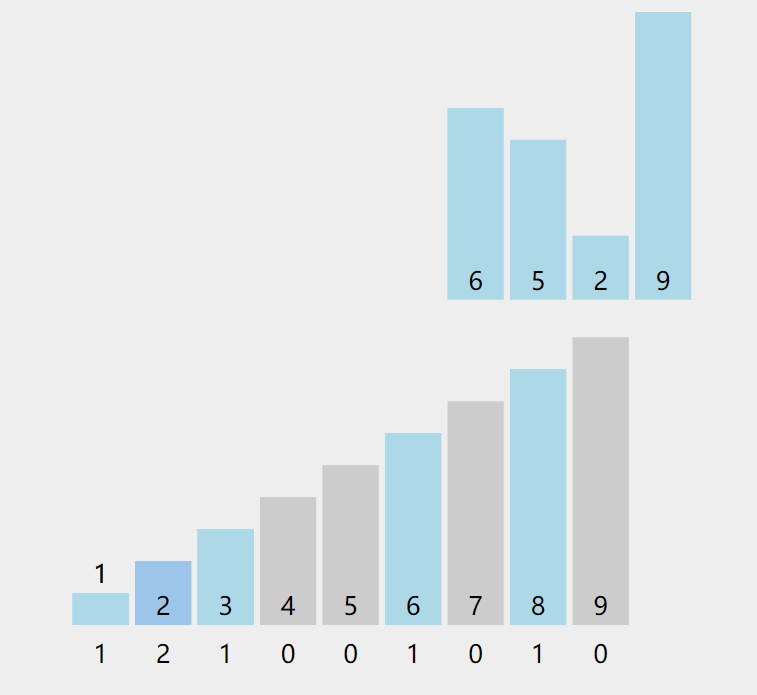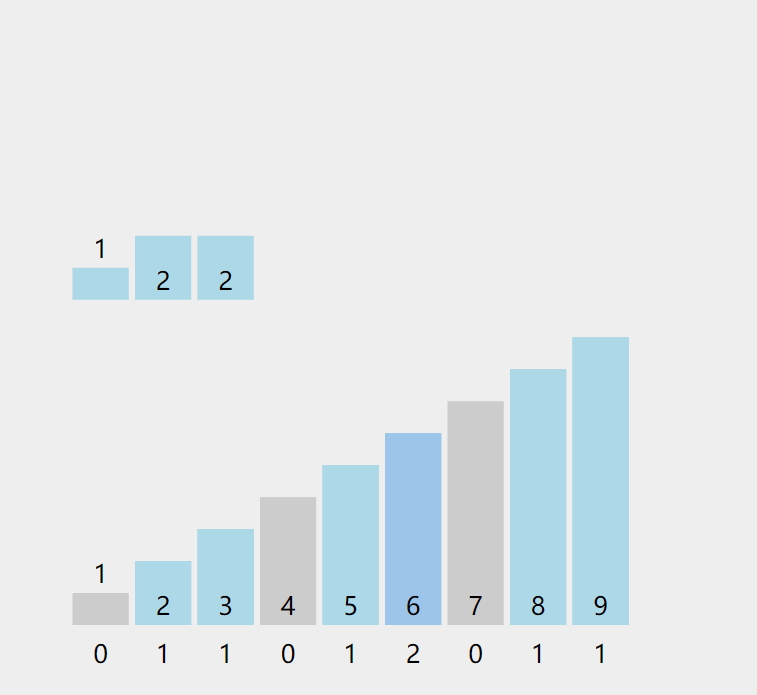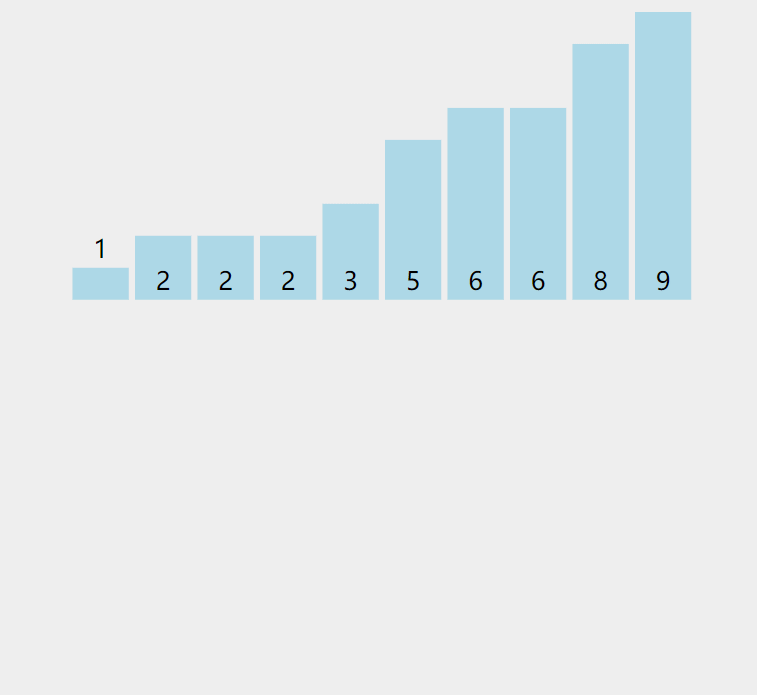
注：图片来自https://visualgo.net，它采用了正序遍历，破坏稳定性，故不推荐

3.算法分析

时间复杂度：

当输入的元素是n个0到k之间的整数时，它的执行时间是O(n+k)

空间复杂度：

需要创建k+1个计数器，空间复杂度为O(k)

稳定性：

分配过程有先后顺序，这是一种稳定的排序方法。

复杂性：

较复杂

本文由 ukuq 创作，采用知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: Feb 2, 2019 at 08:26 pm