AVL树

二叉树 查找 平衡树

二叉排序树中查找操作的执行时间与树形有关系，最坏情况下执行时间为线性（即退化为链表），为了避免这种情况的发生，引入了平衡树的概念。

平衡的二叉树有很多种，其中较为著名的为AVL树，它得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis。

简单定义：

平衡因子：一个节点的平衡因子时该节点的左子树高度减去其右子树高度（或右减去左）。

平衡二叉树：一棵二叉树中每个节点的左右子树高度最多相差1，即该二叉树的每个节点的平衡因子均为1、0或-1。

特殊性：

一般来说，平衡二叉树总是二叉排序树，平衡二叉树是在二叉排序树的基础上增加了树形约束，即要求每个节点是平衡的。

插入删除：

平衡二叉树本质上是二叉排序树，插入和删除基本与二叉排序树一致，只是多了一个调整的步骤：

无论是对一棵平衡树进行插入或是删除操作，都会改变原有节点的平衡因子，有可能使平衡树失衡，因此需要进行必要调整，使其仍是一棵平衡树。

按旋转类型分类：

左旋：

以某一个节点为轴，它的右子枝逆时针旋转，作为新子树的根，称之为逆时针旋转（anticlockwise）或者左旋转。

右旋：

以某一个节点为轴，它的左子枝顺时针旋转，作为新子树的根，称之为顺时针旋转（clockwise）或者右旋转。

调整分为四类，以插入节点引起的失衡为例：

按调整类型分类：

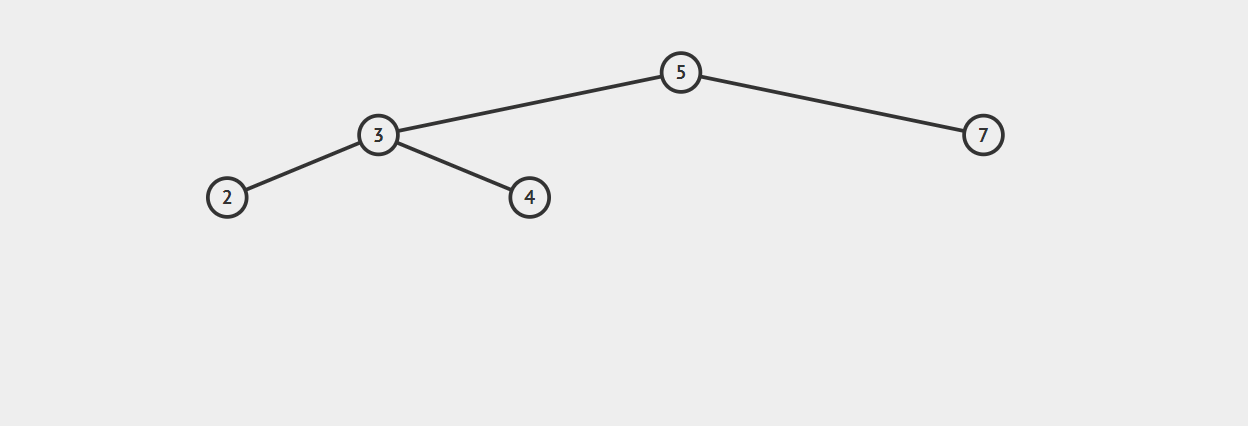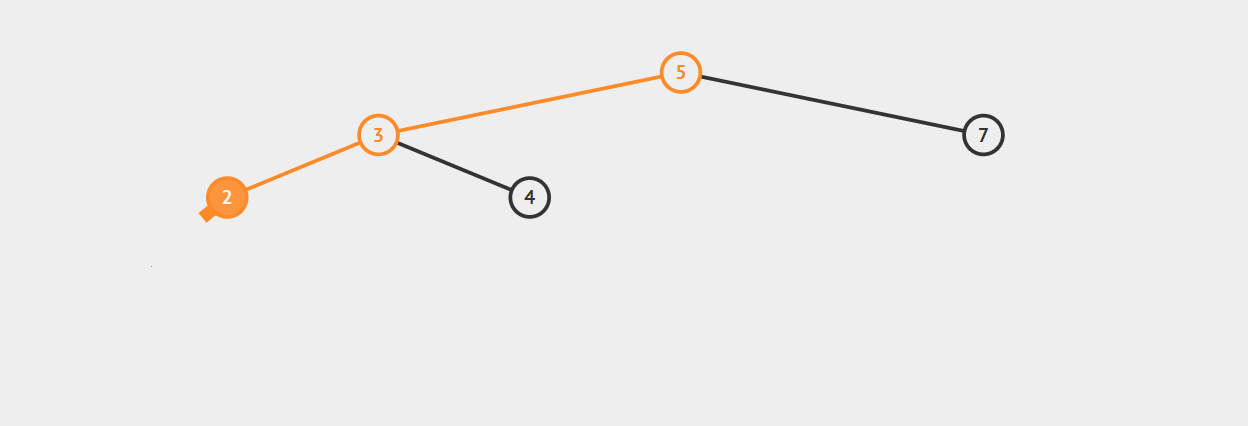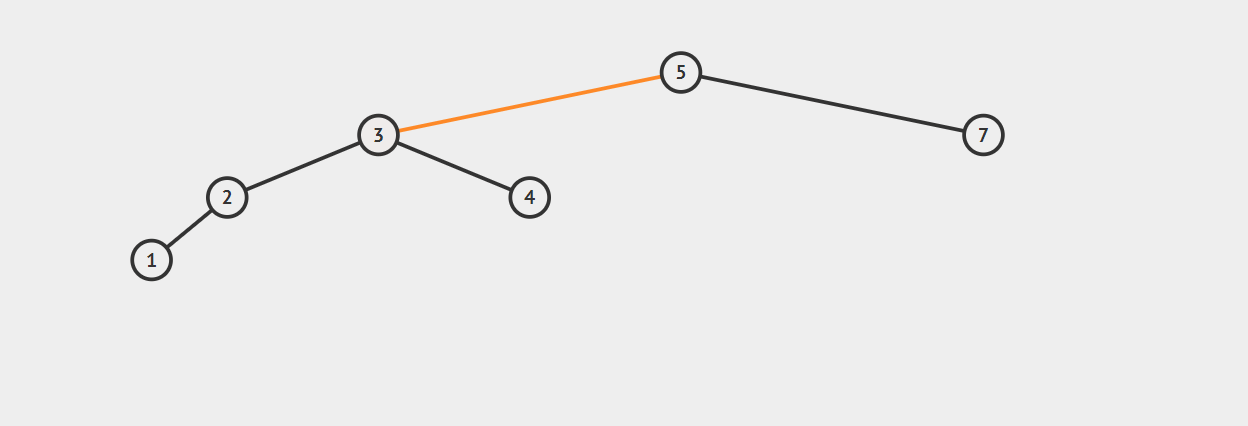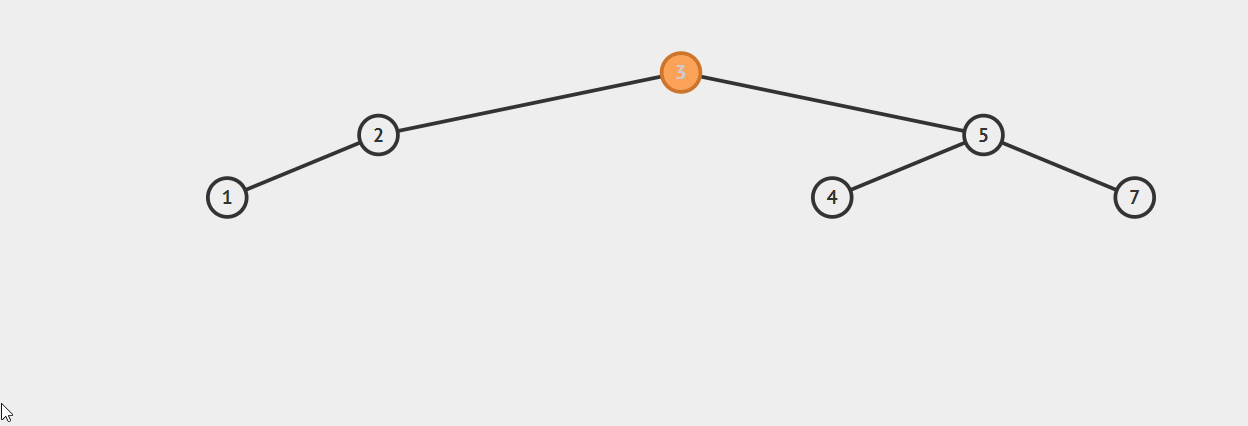
LL型调整：

在节点1插入后，节点5平衡因子变为2（3-1），5-3-2构成LL型不平衡。

右旋转：将3的右子树调整为5的左子树，并将3调整为5的父节点

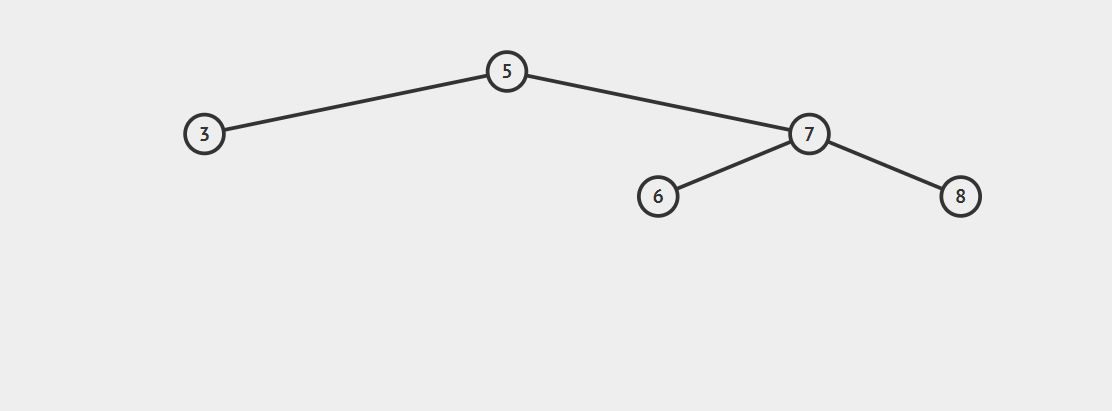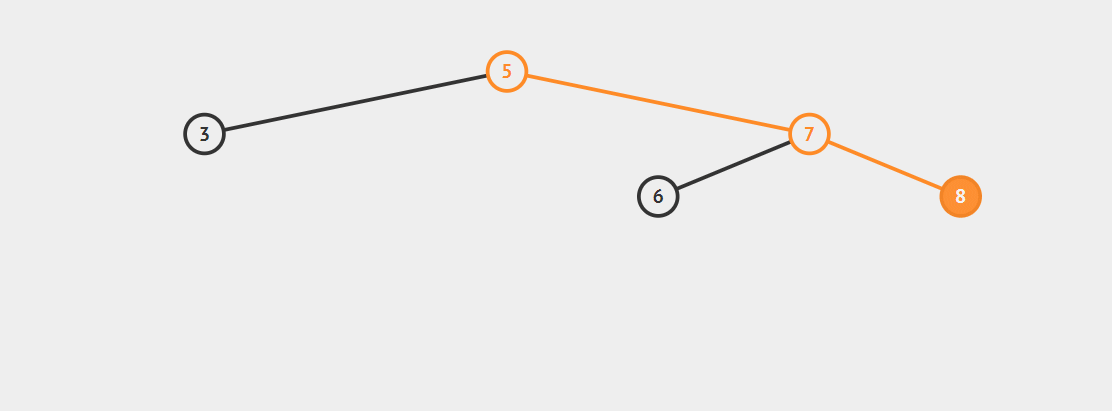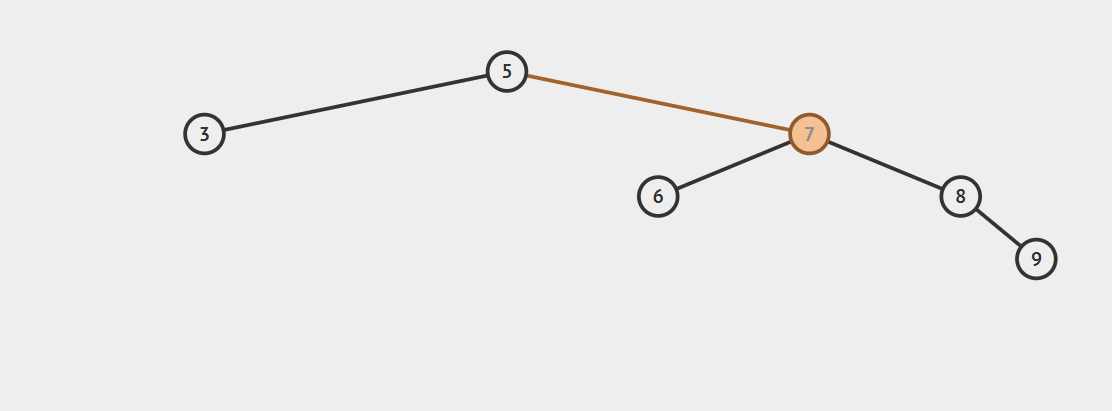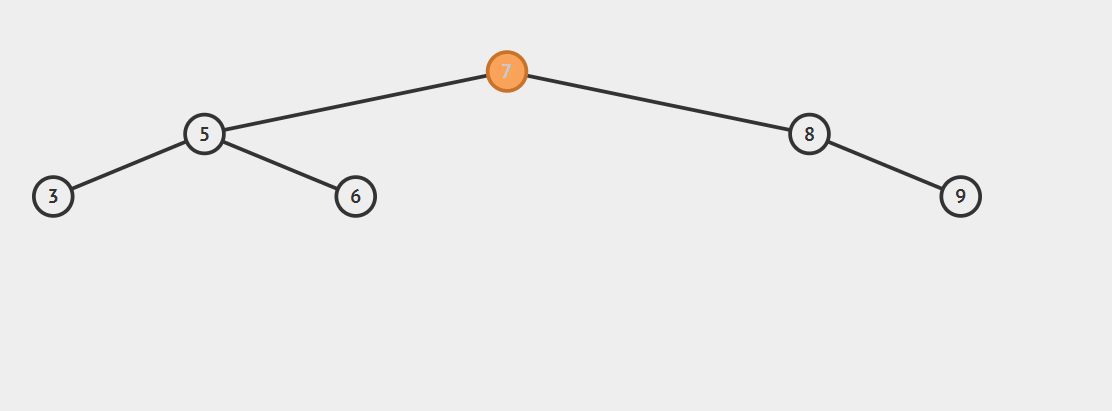
RR型调整：

在节点9插入后，节点5平衡因子变为-2（1-3），5-7-8构成RR型不平衡。

左旋转：将7的左子树调整为5的右子树，并将7调整为5的父节点

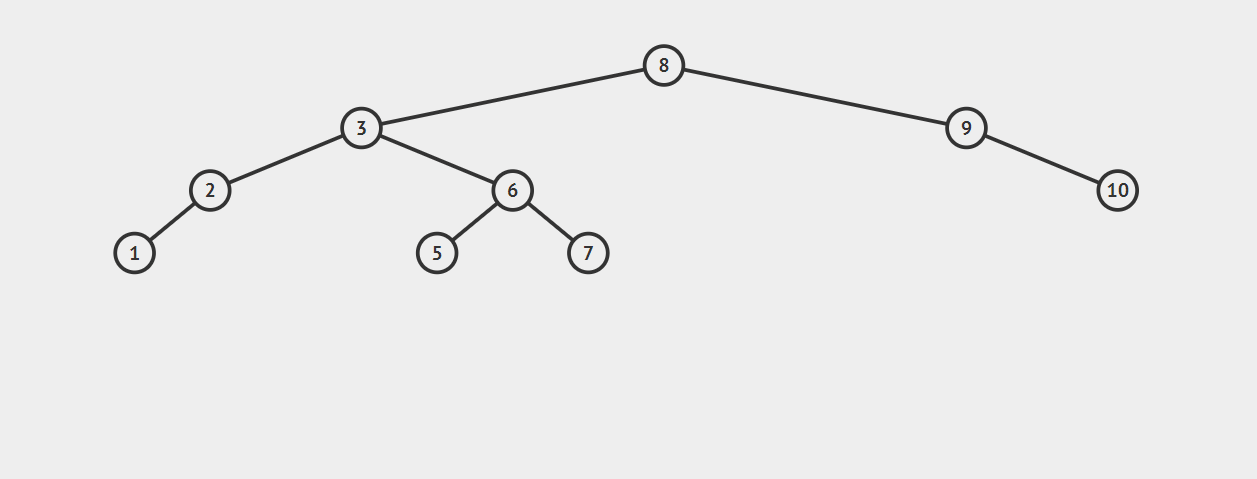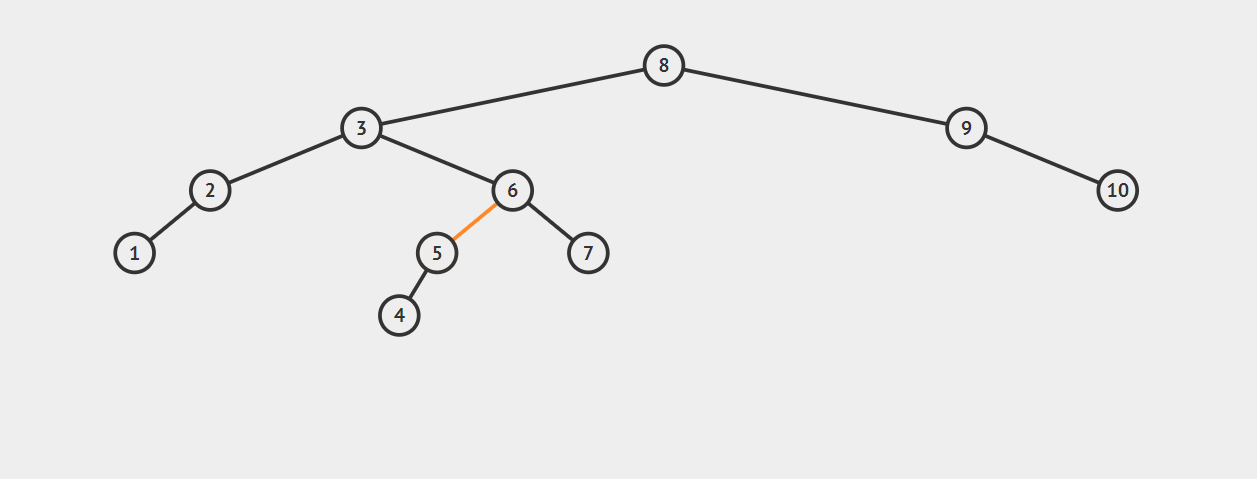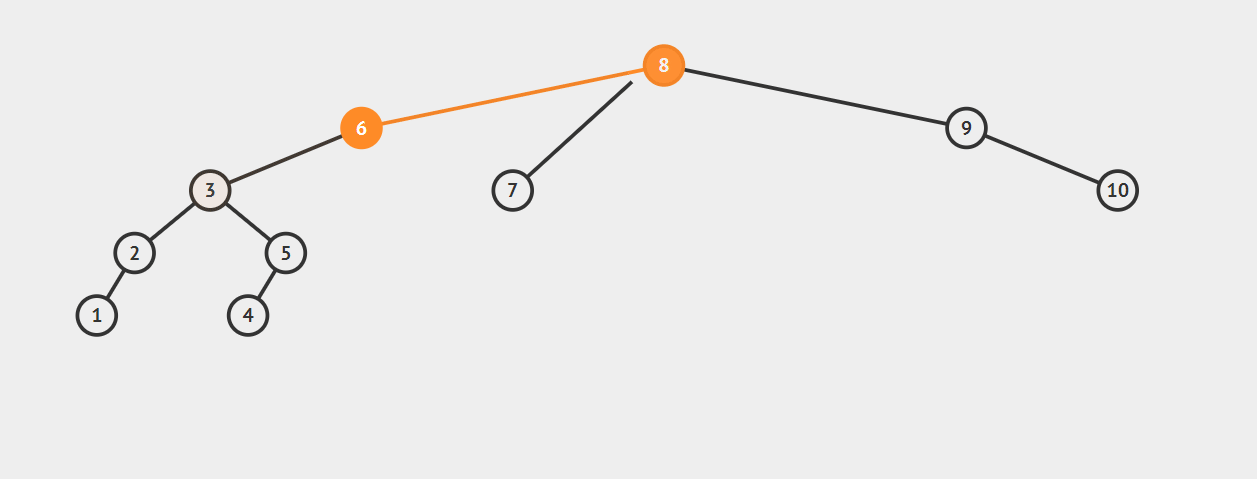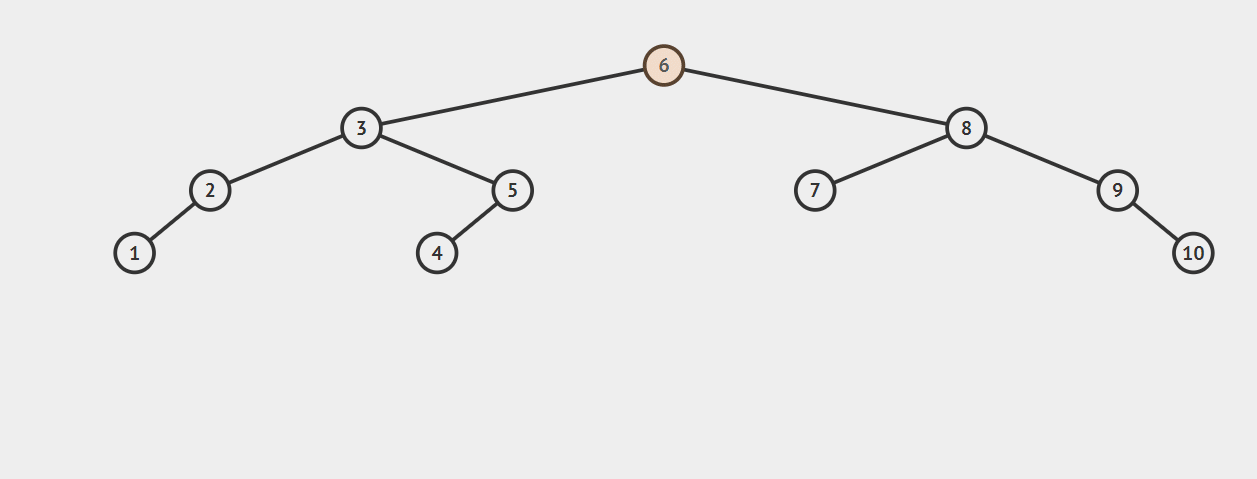
LR型调整：

在节点4插入后，节点8平衡因子变为2（4-2），8-3-6构成LR型不平衡。

先左旋后右旋：将6的左子树调整为3的右子树，将6的右子树调整为8的左子树，并将6调整为3、8的父节点

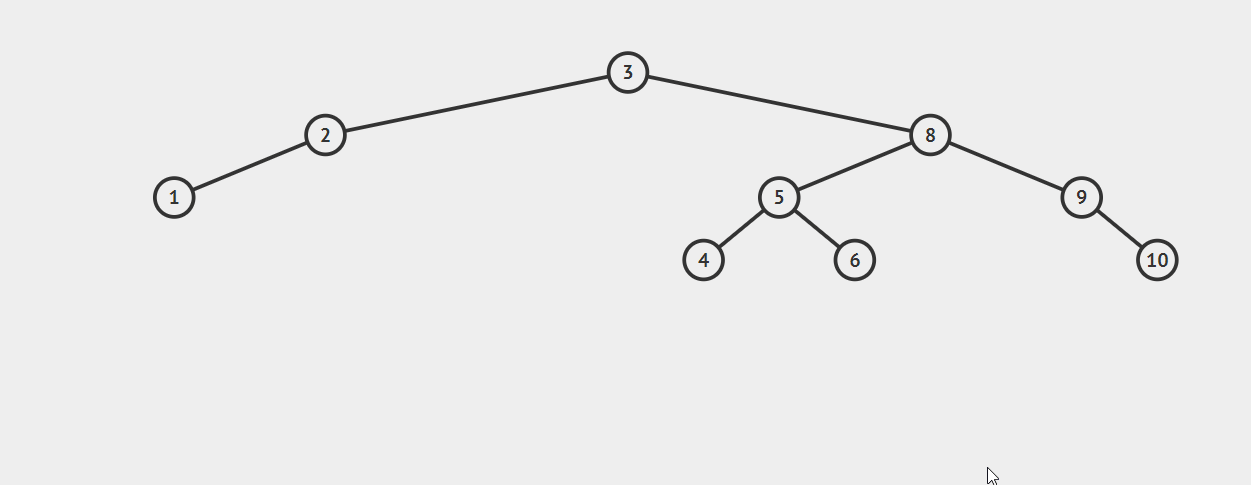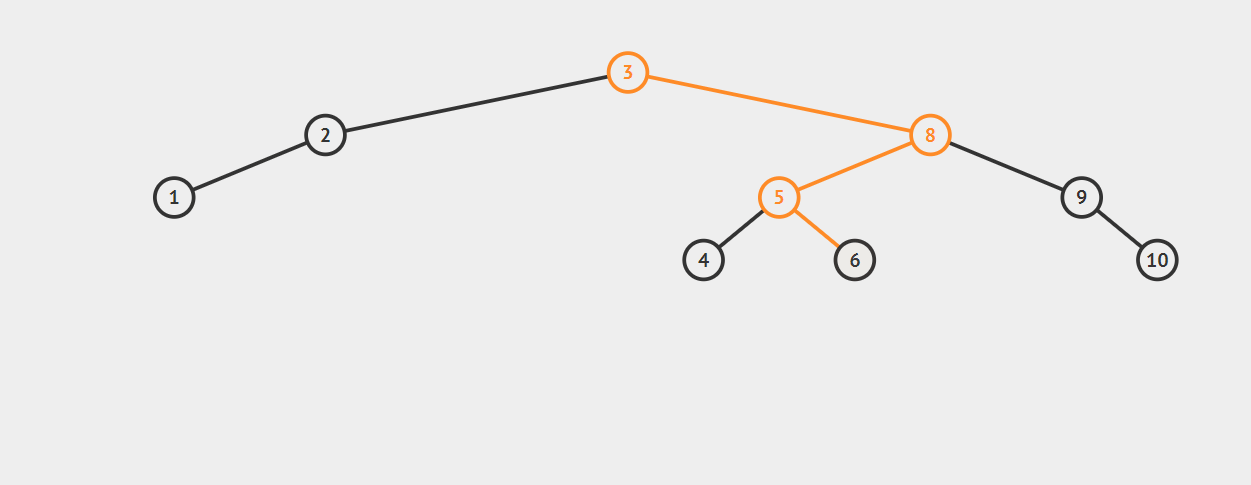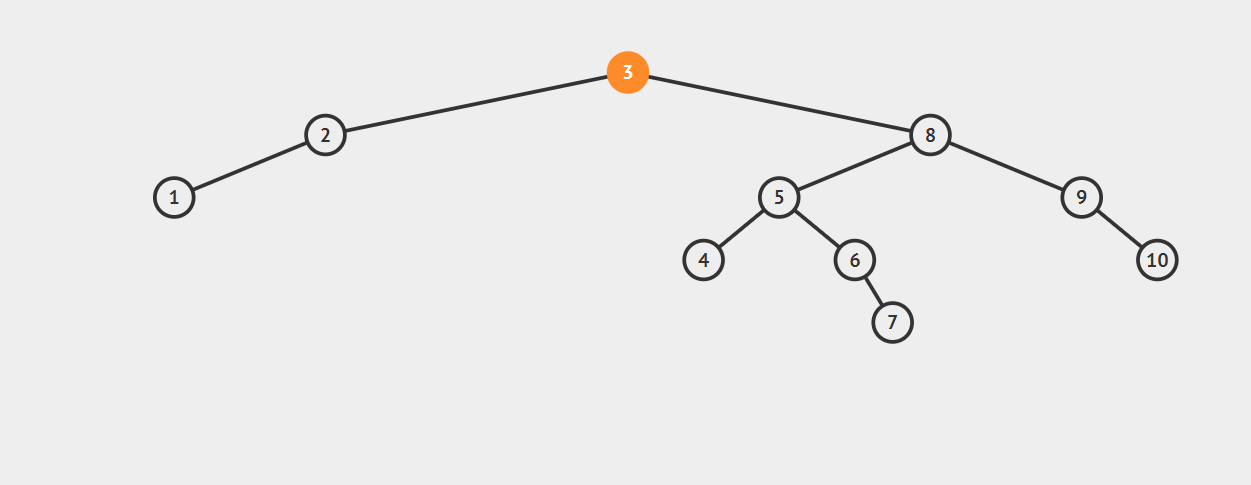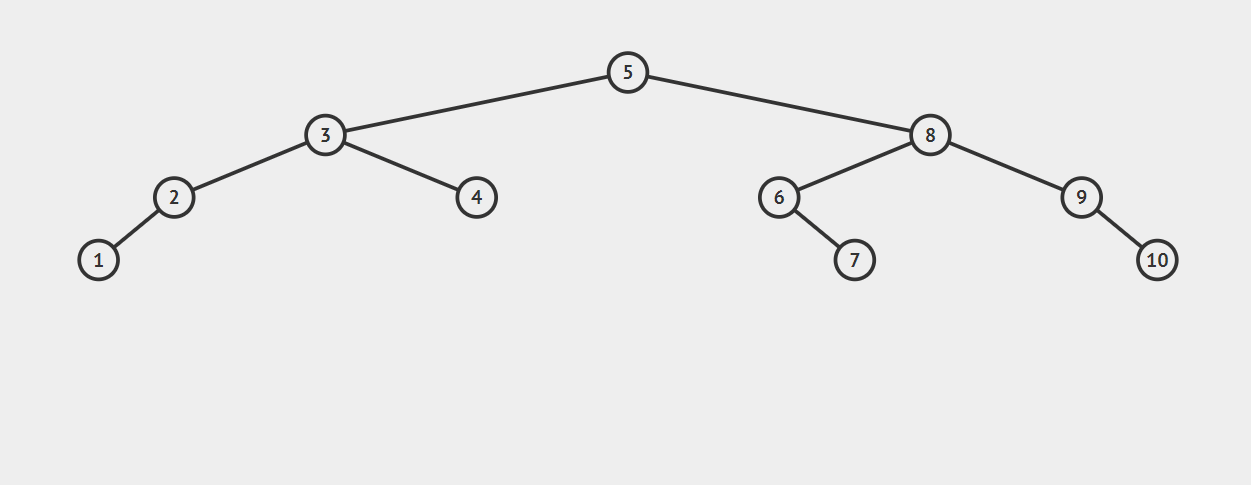
RL型调整：

在节点7插入后，节点3平衡因子变为-2（2-4），3-8-5构成RL型不平衡。

先右旋后左旋：将5的左子树调整为3的右子树，将5的右子树调整为8的左子树，并将5调整为3、8的父节点

本文由 ukuq 创作，采用 知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: Feb 24, 2019 at 11:09 pm